Probabilistic Thinking: The Art of Making Decisions When Nothing Is Certain
Should You Carry an Umbrella? Better Business Decisions in 4 Steps: The Probabilistic Thinking Approach
In this issue:
The Umbrella Dilemma
What is Probabilistic Thinking?
How Probabilistic Thinking Works
Applying Probabilistic Thinking: Real-life Leadership Scenarios
The Probabilistic Thinking Application Worksheet
References
Final Takeaway
⛱
The Umbrella Dilemma
I live in tropical Singapore, and frequently face rainy weather on my way to work.
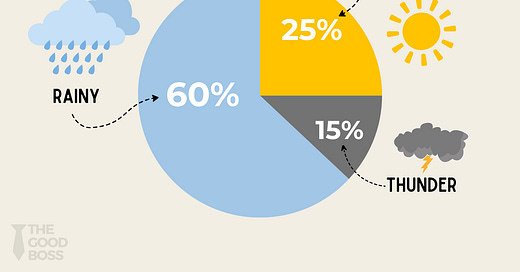
Imagine this: I wake up, check the weather forecast for the day, and see a 60% chance of rain, and a 15% chance of thunderstorms (with the remaining 25% chance of it being a sunny day).
Do I take an umbrella to work?
Most people instinctively react in one of two ways:
Deterministic Thinking: "60% is high—I won’t take my chances and carry one."
All-Or-Nothing Thinking: "There's any chance of rain? Better carry an umbrella just in case!"
But neither of these approaches is optimal. As a probabilistic thinker, I would approach it differently:
If carrying an umbrella has little downside (it’s light and easily fits in my bag) and could prevent discomfort (I don’t like to get drenched, or soaked in the hot sun!), it’s a smart choice.
If the downside of carrying it is high (e.g., it's bulky, I’m biking to work, or I’m only outdoors for a mere 10 mins on my way to work), I might accept the small risk and go without it.
Now, imagine applying this kind of probabilistic reasoning to major business decisions—launching a product, hiring an executive, or investing in innovation.
This is where probabilistic thinking becomes a powerful framework for leaders. It helps you avoid gut-driven decisions and instead make calculated, high-quality choices in an uncertain world.
What is Probabilistic Thinking?
Probabilistic thinking is about assigning likelihoods to different possible outcomes and making decisions based on their probabilities and impact.
Think of it like this:
A deterministic thinker says, “Our product will succeed.”
A probabilistic thinker says, “There’s a 70% chance of success, 20% chance of moderate performance, and 10% chance of failure.”
Going back to the weather example:
Binary thinking: “It will be either rainy, or sunny.”
Probabilistic thinking: “There is a 70% chance of rain.”
Rather than treating decisions as black or white, probabilistic thinkers evaluate a range of possible futures, weigh the risks, and make informed choices.
Poker players, hedge fund managers, and military strategists use probabilistic thinking daily.
As a leader, you should too.
How Probabilistic Thinking Works
Probabilistic thinking involves four key steps:
1. Recognize Uncertainty
Accept that no decision has a 100% guaranteed outcome.
Identify multiple possible results and what influences them.
2. Assign Probabilities to Different Outcomes
Estimate the likelihood of success, moderate success, and failure based on available data.
3. Calculate Expected Value (EV)
Weigh potential benefits and risks against their probabilities.
Use this formula:
EV = (Probability of Success × Reward) + (Probability of Moderate Success × Reward) + (Probability of Failure × Loss)
4. Update Probabilities as New Data Emerges (Bayesian Thinking)
Probabilities and outcomes may change over time.
Adjust probabilities based on customer feedback, market trends, and test results.
Applying Probabilistic Thinking: Real-life Leadership Scenarios
Now, let’s discuss how probabilistic thinking can be applied in four specific real-world leadership scenarios.
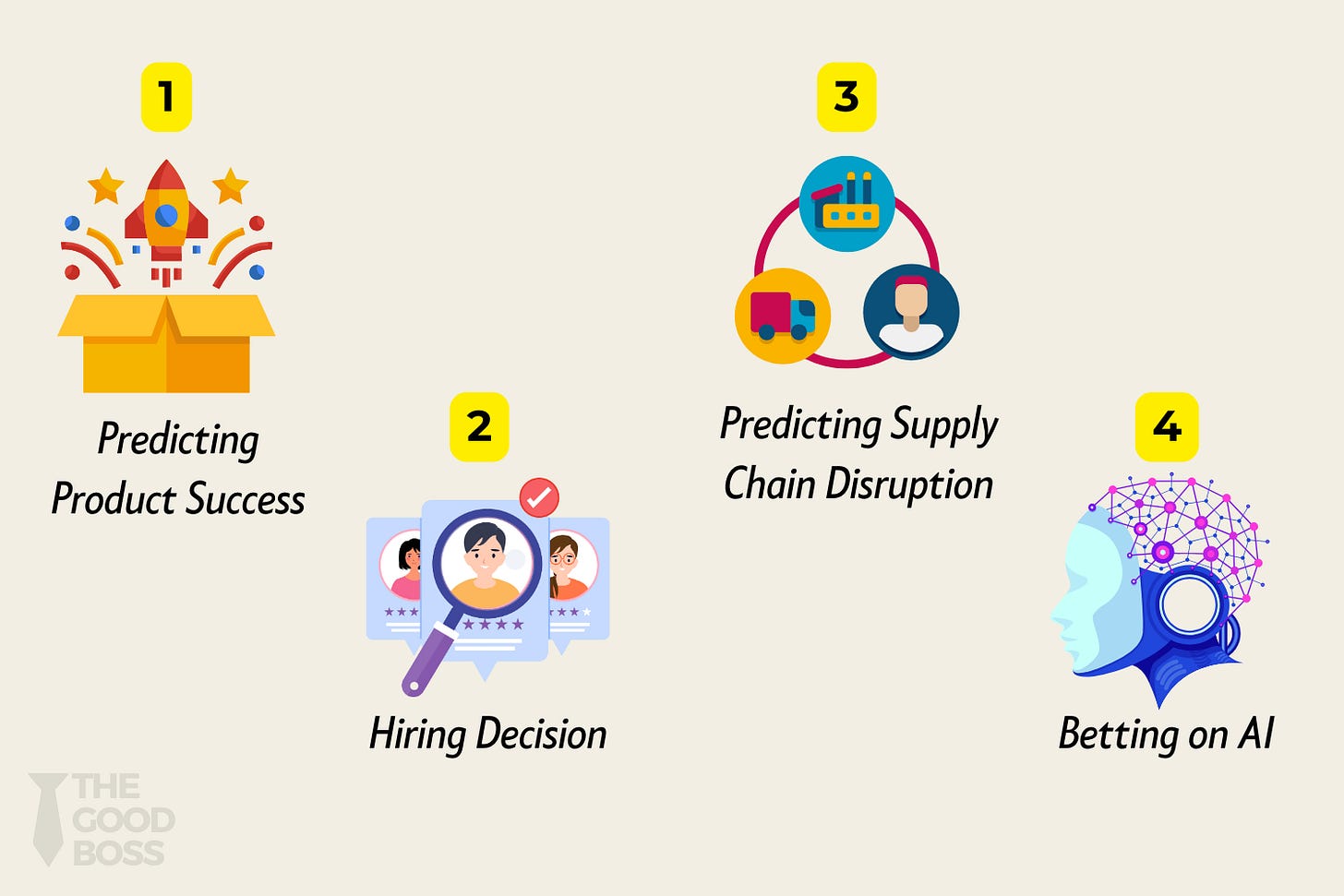
1. Business Strategy: Predicting Product Success
Scenario: Your company is launching a new software product. Past launches show that:
50% of similar products perform well and generate $5M in revenue.
30% perform moderately, earning $2M.
20% fail, losing $1M.
Expected Value Calculation:
EV = (0.50×5M) + (0.30×2M) + (0.20×−1M) = 2.9M
Conclusion:
👉🏼 Even with the risk of failure, the product has a positive expected value of $2.9M—indicating it’s a good investment.
2. Hiring Decisions: Selecting the Right Candidate
Scenario: You’re hiring for a leadership position. Based on data from past hires:
60% of candidates with similar profiles excel, contributing $500K in value over 3 years.
30% perform adequately, generating $200K.
10% underperform, costing the company $100K in losses.
Expected Value Calculation:
EV = (0.60×500K) + (0.30×200K) + (0.10×−100K) = 350K
Conclusion:
👉🏼 A positive $350K expected value suggests the candidate is a strong hire.
Consider this slightly different scenario: Let’s say this is a highly critical position, and the risk of hiring the wrong person could incur a loss of $4M, the EV calculation would look like this:
EV = (0.60×500K) + (0.30×200K) + (0.10×−4M) = -40K
Conclusion:
👉🏼 This is a negative expected value, and probabilistic thinking suggests the candidate should not be hired.
💡As you can tell, changing the values of the probabilities and outcomes can influence the final decision, so you should pay close attention to how you arrive at the values of the probabilities and outcomes in the first place.
3. Crisis Management: Navigating a Supply Chain Disruption
Scenario: Your company depends on a single supplier for a critical component. A geopolitical event creates uncertainty, leading to:
40% chance of no disruption (zero financial loss).
40% chance of delays, costing $2M in lost revenue.
20% chance of a complete failure, costing $5M.
Expected Value Calculation:
EV = (0.40×0) + (0.40×−2M) + (0.20×−5M) = −1.8M
Conclusion:
👉🏼 With an expected loss of $1.8M, taking preventative action is necessary.
4. Investing in Innovation: Should We Bet on AI?
Scenario: With all the buzz and energy around AI, your company is considering a $3M investment in AI-driven automation.
50% probability of high success, generating $10M.
30% probability of moderate success, earning $5M.
20% probability of failure, losing the full $3M.
Expected Value Calculation:
EV = (0.50×10M) + (0.30×5M) + (0.20×−3M) = 5.9M
Conclusion:
👉🏼 With a positive $5.9M expected value, the investment is worth pursuing.
The Probabilistic Thinking Application Worksheet
Now that we have a good understanding of the framework, it’s time to put this learning into practice!
Download the Probabilistic Thinking Application Worksheet and use it to:
Make Smarter Decisions – Assess risks and rewards using probabilities instead of relying on gut feelings.
Minimize Risk, Maximize Gain – Use Expected Value (EV) to prioritize high-impact decisions and avoid costly mistakes.
Stay Agile & Adapt – Continuously update your estimates as new data emerges to improve decision accuracy.
The worksheet includes step-by-step prompts to guide you through the entire application process.
⬇️ Download Your Worksheet Here!
🎁 Paid Subscribers: Claim your FREE copy of this worksheet by using the exclusive coupon code mentioned on this page. Not a paid member? You can upgrade here.
References
Thinking in Bets by Annie Duke: A former poker pro explains how to embrace uncertainty and make smarter decisions by thinking in probabilities. A go-to reference for applying probabilistic thinking in everyday leadership.
Superforecasting by Philip Tetlock & Dan Gardner: Explores how some people become incredibly accurate at predicting uncertain events. Practical for leaders who want to sharpen their decision-making in complex environments.
The Signal and the Noise by Nate Silver: A deep dive into why most predictions fail and how probabilistic thinkers separate meaningful signals from noise.
Final Takeaway
The smartest decisions aren’t the safest—they’re the ones made with clear eyes and calculated risks.
Probabilistic thinking won’t give you certainty—but it will give you control.
Control over how you evaluate choices.
Control over how you respond to change.
And control over the quality of your leadership when the path ahead is uncertain.
So the next time you’re in the middle of uncertainty:
Take a pause.
Weigh the odds.
Make your smart bet.
What’s your biggest takeaway from this approach to decision-making? Let me know in the comments!
Other posts you will enjoy
👋🏻 Let’s stay in touch - connect with me on LinkedIn.
PS: If you’re enjoying The Good Boss, will you take 2 seconds and hit the ❤️ button and share/restack 🔁 it with others who might find it helpful? It goes a long way in helping me grow the newsletter. Thank you!








I love this framework!
One question that I have- on the surface it feels to me like there is a slight bias towards success in the calculations, since we have a positive outcome and a moderately positive outcome but only one negative outcome. Is there an explanation for this? Intuitively it seems that if we added more "tiers" we'd get more precision, though they'd probably be harder to define then the 3 you have outlined